「VK Cup 2015-Round 2」A.Berland Miners /「ZJOI模拟赛」俄刻阿诺斯

发表于 | 分类于 | | 浏览量： 次

没想到蒟蒻我有生之年竟然也能A上一道VK CUP的题。

传送门

原题链接：

CF533A

洛谷

数据范围与时有所不同。

下文中的B数组就是棒子的长度。

题解

首先考虑没有开凿操作时，如何判断当前的情况是否合法。

不难发现，能否将一根棒子放进一个洞穴里，取决于该洞穴到根中高度最小的节点，设每个节点到根节点路径上高度最小值为$Min[i]​$（可以$O(n)​$构造出来）。对$Min​$和$B​$两个数组分别从小到大排序。

当满足$B[i] \leq Min[j]$时，棒子$i$就可以放进洞穴$j$里。设第$i$根棒子可以放进$num[i]$个洞穴。当满足$\forall i,num[i]\geq i$时，就合法。也就是当且仅当$\min_{i=1}^{n}{(num[i]-i)}\geq 0$时合法。

然后考虑开凿操作。由于不知道开凿哪一个节点，那么$O(n)​$枚举过去。然后二分要开凿的高度。

1.png

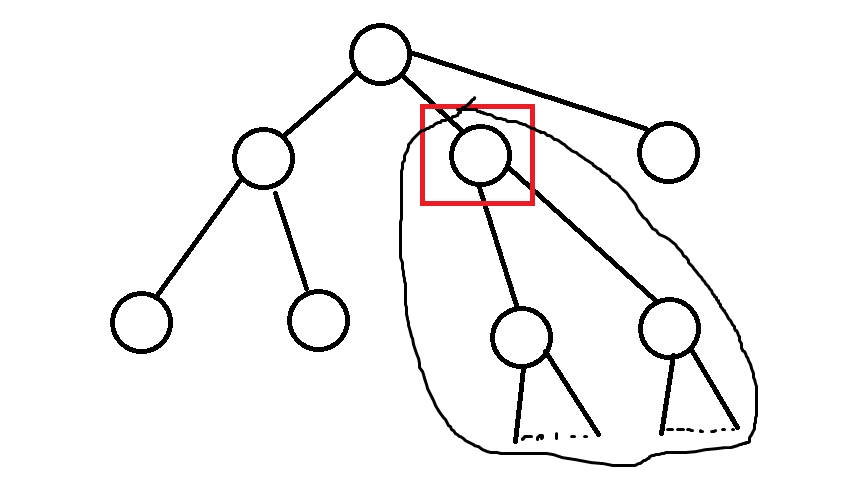
比如要对图中这个节点进行开凿，那么它的子树中的以该节点为最小值的节点的$Min$值就会改变，所以$Min$数组中就可能需要删去几个原先的值然后加入几个新元素（可能加入二分后的高度或原先到根节点链上的次小值），由于$Min$数组中的每一个元素都对$num$数组中一个连续区间产生贡献，且删除一个元素后一整个区间的值被减1，加入一个元素后一整个区间的值被加1，所以就套个线段树维护全局最小值即可。并且由于每个节点到树根的链上只有一个最小值，所以对于每一个节点，只有一个节点在二分的时候会影响到它，所以时间复杂度为$O(n\log n \log B_i)$。

然后蒟蒻我傻呵呵地卡了半天常数，死活过不去，只好想$O(n\log n)$的做法。

经过ZZK大佬的点拨，我发现其实根本不需要二分。

找到最长的$num_i-B_i$的值小于零的棒子，那么如果有解，就一定要将某个洞穴的高度开凿到这根棒子的长度。

于是乎就可以$O(n)$枚举开凿哪一个洞穴，然后检查一下开凿完之后是否合法就好了。

代码

下面是两个log的代码（贼慢）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=200005,inf=0x3F3F3F3F;
int n,m,tot,lnk[maxn],w[maxn],son[maxn*2],nxt[maxn*2],B[maxn],Min[maxn],Sec[maxn],tot2,lnk2[maxn],son2[maxn],nxt2[maxn],L,R=inf,mid;
inline int read()
{
	int ret=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=getchar();}
	return ret*f;
}
inline void add_e(int x,int y){tot++;son[tot]=y;nxt[tot]=lnk[x];lnk[x]=tot;}
inline void add_e2(int x,int y){tot2++;son2[tot2]=y;nxt2[tot2]=lnk2[x];lnk2[x]=tot2;}
struct SegmentTree
{
	struct Node{int Min,Tag;}Tree[maxn*4];
	void PushUp(int rt){Tree[rt].Min=min(Tree[rt*2].Min,Tree[rt*2+1].Min);}
	void PushDown(int rt)
	{
		if(!Tree[rt].Tag) return;
		Tree[rt*2].Min+=Tree[rt].Tag;Tree[rt*2+1].Min+=Tree[rt].Tag;
		Tree[rt*2].Tag+=Tree[rt].Tag;Tree[rt*2+1].Tag+=Tree[rt].Tag;
		Tree[rt].Tag=0;
	}
	void RangeUpdate(int LL,int RR,int delta,int L=1,int R=m,int rt=1)
	{
		if(LL<=L&&R<=RR){Tree[rt].Min+=delta;Tree[rt].Tag+=delta;return;}
		PushDown(rt);
		int M=(L+R)/2;
		if(LL<=M) RangeUpdate(LL,RR,delta,L,M,rt*2);
		if(M<RR) RangeUpdate(LL,RR,delta,M+1,R,rt*2+1);
		PushUp(rt);
	}
	void Build(int L=1,int R=m,int rt=1)
	{
		if(L==R){Tree[rt].Min=L-m-1;return;}
		int M=(L+R)/2;
		Build(L,M,rt*2);
		Build(M+1,R,rt*2+1);
		PushUp(rt);
	}
	int QueryAll(){return Tree[1].Min;}
}T;
void Build(int now,int fa,int id,int mi,int se)
{
	if(w[now]<=mi){se=mi;mi=w[now];id=now;}
	else if(w[now]<se) se=w[now];
	Min[now]=mi;Sec[now]=se;add_e2(id,now);
	for(int i=lnk[now];i;i=nxt[i])
		if(son[i]!=fa)
			Build(son[i],now,id,mi,se);
}
inline void Modify(int num,int delta)
{
	static int L,R,mid;
	L=1;R=m;
	while(L<=R)
	{
		mid=(L+R)/2;
		B[mid]<=num?L=mid+1:R=mid-1;
	}
	if(R>=1) T.RangeUpdate(1,R,delta);
}
inline bool Check(int now,int fa)
{
	for(int i=lnk2[now];i;i=nxt2[i])
	{
		Modify(Min[now],-1);
		Modify(min(Sec[son2[i]],w[now]+mid),1);
	}
	bool flg=false;
	if(T.QueryAll()>=0) flg=true;
	for(int i=lnk2[now];i;i=nxt2[i])
	{
		Modify(Min[now],1);
		Modify(min(Sec[son2[i]],w[now]+mid),-1);
	}
	if(flg) return true;
	for(int i=lnk[now];i;i=nxt[i])
		if(son[i]!=fa&&Check(son[i],now))
			return true;
	return false;
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++) w[i]=read();
	for(int i=2;i<=n;i++)
	{
		int a=read(),b=read();
		add_e(a,b);add_e(b,a);
	}
	m=read();
	for(int i=1;i<=m;i++) B[i]=read();
	sort(B+1,B+1+m);
	Build(1,0,0,inf,inf);
	T.Build();
	for(int i=1;i<=n;i++) Modify(Min[i],1);
	while(L<=R)
	{
		mid=(L+R)/2;
		Check(1,0)?R=mid-1:L=mid+1;
	}
	printf("%d\n",L<inf?L:-1);
	return 0;
}

一个log的代码（跑的飞快）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=200005,inf=0x3F3F3F3F;
int n,m,tot,lnk[maxn],w[maxn],son[maxn*2],nxt[maxn*2],B[maxn],Min[maxn],Sec[maxn],tot2,lnk2[maxn],son2[maxn],nxt2[maxn],BMax,ans=inf;
inline char nc()
{
	static char buf[8388608],*L=buf,*R=buf;
	return L==R&&(R=(L=buf)+fread(buf,1,8388608,stdin),L==R)?EOF:*L++;
}
inline int read()
{
	int ret=0,f=1;char ch=nc();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=nc();}
	while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=nc();}
	return ret*f;
}
inline void add_e(int x,int y){tot++;son[tot]=y;nxt[tot]=lnk[x];lnk[x]=tot;}
inline void add_e2(int x,int y){tot2++;son2[tot2]=y;nxt2[tot2]=lnk2[x];lnk2[x]=tot2;}
struct SegmentTree
{
	struct Node{int Min,Tag;}Tree[maxn*4];
	inline void PushUp(int rt){Tree[rt].Min=(Tree[rt<<1].Min<Tree[rt<<1|1].Min?Tree[rt<<1].Min:Tree[rt<<1|1].Min);}
	inline void PushDown(int rt)
	{
		if(!Tree[rt].Tag) return;
		Tree[rt<<1].Min+=Tree[rt].Tag;Tree[rt<<1|1].Min+=Tree[rt].Tag;
		Tree[rt<<1].Tag+=Tree[rt].Tag;Tree[rt<<1|1].Tag+=Tree[rt].Tag;
		Tree[rt].Tag=0;
	}
	inline void RangeUpdate(int RR,int delta,int L=1,int R=m,int rt=1)
	{	
		if(RR==m){Tree[rt].Min+=delta;Tree[rt].Tag+=delta;return;}
		while(L<=R&&L<=RR)
		{
			PushDown(rt);
			int M=(L+R)>>1;
			if(M<=RR){Tree[rt<<1].Min+=delta;Tree[rt<<1].Tag+=delta;L=M+1;rt=rt<<1|1;}
			else{R=M;rt=rt<<1;}
		}
		while(rt>1){rt>>=1;PushUp(rt);}
	}
	void Build(int L=1,int R=m,int rt=1)
	{
		if(L==R){Tree[rt].Min=L-m-1;return;}
		int M=(L+R)>>1;
		Build(L,M,rt<<1);
		Build(M+1,R,rt<<1|1);
		PushUp(rt);
	}
	inline int Query(int pos,int L=1,int R=m,int rt=1)
	{
		if(L==R) return Tree[rt].Min;
		int M=(L+R)>>1;
		PushDown(rt);
		if(pos<=M) return Query(pos,L,M,rt<<1);
		else return Query(pos,M+1,R,rt<<1|1);
	}
}T;
void Build(int now,int fa,int id,int mi,int se)
{
	if(w[now]<=mi){se=mi;mi=w[now];id=now;}
	else if(w[now]<se) se=w[now];
	Min[now]=mi;Sec[now]=se;add_e2(id,now);
	for(int i=lnk[now];i;i=nxt[i])
		if(son[i]!=fa)
			Build(son[i],now,id,mi,se);
}
inline void Modify(int num,int delta)
{
	int L=1,R=m,mid;
	while(L<=R)
	{
		mid=(L+R)>>1;
		B[mid]<=num?L=mid+1:R=mid-1;
	}
	if(R>=1) T.RangeUpdate(R,delta);
}
inline void Solve(int now,int fa)
{
	if(w[now]<BMax&&BMax-w[now]<ans)
	{
		for(int i=lnk2[now];i;i=nxt2[i])
		{
			Modify(Min[now],-1);
			Modify(min(Sec[son2[i]],BMax),1);
		}	
		if(T.Tree[1].Min>=0) ans=BMax-w[now];
		for(int i=lnk2[now];i;i=nxt2[i])
		{
			Modify(Min[now],1);
			Modify(min(Sec[son2[i]],BMax),-1);
		}
	}
	for(int i=lnk[now];i;i=nxt[i])
		if(son[i]!=fa)
			Solve(son[i],now);
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++) w[i]=read();
	for(int i=2;i<=n;i++)
	{
		int a=read(),b=read();
		add_e(a,b);add_e(b,a);
	}
	m=read();
	for(int i=1;i<=m;i++) B[i]=read();
	sort(B+1,B+1+m);
	Build(1,0,0,inf,inf);
	T.Build();
	for(int i=1;i<=n;i++) Modify(Min[i],1);
	for(int i=m;i;i--)
		if(T.Query(i)<0)
			{BMax=B[i];break;}
	if(BMax) Solve(1,0);
	else ans=0;
	printf("%d\n",ans==inf?-1:ans);
	return 0;
}